Through the Looking Class: Contravariant Functors and Applicatives
Siddharth Bhat
16 Mar 2021
•
7 min read
In this blog post, we will learn about Contravariant and
Divisible which provide duals for Data.Functor and Data.Applicative
respectively.
{-# LANGUAGE NoImplicitPrelude #-}
{-# LANGUAGE InstanceSigs #-}
import GHC.Base hiding (Functor)
import GHC.Float -- for Ord instance of Float
import GHC.Show -- for show
Dual Functors
First, a quick recap of functors:
class Functor f where
fmap :: (a -> b) -> f a -> f b
This lets us lift a function f: a -> b into a fmap f: f a -> f b.
The dual is called Contravariant:
class Contravariant f where
contramap :: (a -> b) -> f b -> f a
Let us look at some example to build our intuition of such a typeclass.
Predicates
The classic example is that of a predicate, which is something that
tells us whether a value of type t obeys some property or not:
data Predicate t = Predicate { runPredicate :: t -> Bool }
instance Contravariant Predicate where
contramap :: (a -> b)
-> Predicate b -- b -> Bool
-> Predicate a -- a -> Bool
contramap a2b (Predicate b2bool) =
Predicate (\a -> b2bool (a2b a))
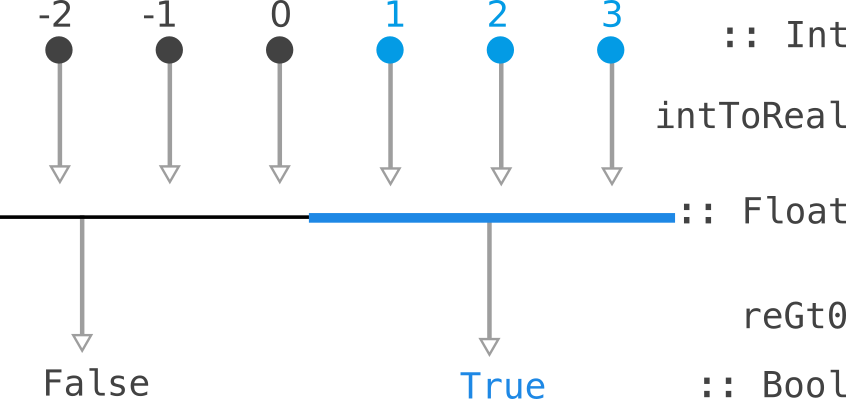
An example of such a thing is if we know how to check a real number is greater than zero:
reGt0 :: Predicate Float
reGt0 = Predicate (\x -> x > 0.0)
and we can converts integers into reals:
intToReal :: Int -> Float
intToReal i = error "TODO" -- fromIntegral
then we can check if an integer is greater than zero:
intGt0 :: Predicate Int
intGt0 = contramap intToReal reGt0
This is described by the picture:
So, such a Predicate Float "consumes" a Float to produce a Bool.
We can pull back the consumption along a function Int -> Float to consume
a Int and produce a Bool.
Dual Applicatives
class Functor f => Applicative f where
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
Recall that an Applicative allow us to work with
tuples:
liftA2 :: (a -> b -> c) -> f a -> f b -> f c
We can write the type of liftA2 to be more suggestive as:
liftA2 :: ((a, b) -> c) -> ((f a, f b) -> f c)
If we can combine a tuple (a, b) into a value c,
then we can glue lifted values (f a, f b) into a lifted f c.
The dual, called Divisible, says that if we can break a value c into (a, b),
then we can glue lifted values (f a, f b) into a lifted f c.
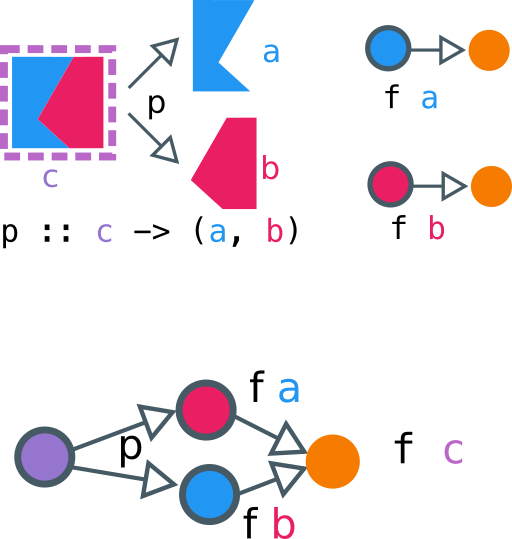
class Contravariant f => Divisible f where
divide :: (c -> (a, b)) -> f a -> f b -> f c
conquer :: f a
The conquer is some sort of "default procedure" we can perform for
any value. It'll be something benign, as we'll see when we check out the examples.
Above, we have a picture of how to think about Divisible. The box with pink-and-blue is a c, that contains an a and a b. We have a function p that shows us how to split a c into an a and a b. We also have f a and f b, which consume a, b to produce some orange output. If we have this data, we can build an f c, something that can consume a c, by (1) splitting c into (a, b), and then consuming the (a, b) using f a and f b.
Example 1: Predicates
We can continue our example of predicates. If we know how to check if
something holds for a and something holds for b, we can check how something
holds for (a, b): check for both a and b. So, this would be:
instance Divisible Predicate where
divide :: (c -> (a, b)) ->
Predicate a -> Predicate b -> Predicate c
divide c2ab (Predicate a2bool) (Predicate b2bool) =
Predicate (\c -> let (a, b) = c2ab c
in a2bool a && b2bool b)
As for when we know nothing, we could either allow it or disallow it.
In this case, since we are && ing information, the way to be "benign"
is to allow things (that is, return a True). Since True && b = b,
we are sure that the conquer is indeed benign.
conquer :: Predicate a
conquer = Predicate (\a -> True)
Example 2: Serialization
Consider the ability to convert a data type to a string. These "consume" the (varying)
data types to produce a String. So, for example:
data Serializer a = Serializer { serialize :: a -> String }
If we know how to print an b (that is, we have b2string :: b-> String),
and we can turn a's into bs, we compose the two to print as:
instance Contravariant Serializer where
contramap :: (a -> b) -> Serializer b -> Serializer a
contramap a2b (Serializer b2string) =
Serializer (\a -> b2string (a2b a))
For our Divisible instance, if we can print a and b, and we
can break a c into an (a, b), we (1) break the c down, and then
(2) print the a and the b, and (3) concatenate the string representation
of a and b:
instance Divisible Serializer where
divide :: (c -> (a, b))
-> Serializer a
-> Serializer b
-> Serializer c
divide c2ab (Serializer a2str) (Serializer b2str) =
Serializer (\c -> let (a, b) = c2ab c
in (a2str a) <> (b2str b))
As for conquer, if we don't know how to print something, the best thing
to do is to not print anything at all. This prevents us from garbling output.
Thus, the benign choice for conquer is to print an empty string:
conquer :: Serializer a
conquer = Serializer (\a -> "")
We can put Serializer work immediately. For example, say we know
how to serializer Ints and Floats:
intSerial :: Serializer Int
intSerial = Serializer (\i -> show i)
floatSerial :: Serializer Float
floatSerial = Serializer (\f -> show f)
If we now have a type that contains Int and Float, no problem! Divisible
has our back to combine the Serializers together:
data Foo = Foo Int Float
fooSerial :: Serializer Foo
fooSerial = divide (\(Foo i f) -> (i, f))
intSerial floatSerial
Example 3 / Generalization: Fixed output type
We can generalize both examples: we have seen before:
Predicate is all functions into a fixed output
type Bool, while Serializer is functions into a fixed output type String. We need
to know how to combine the outputs --- in the case of Bool, we combined the outputs
with &&. In the case of String, we combined the outputs with <>. In general,
we need a monoid.
data Into y x = Into { runInto :: x -> y }
instance Contravariant (Into y) where
contramap :: (b -> a)
-> Into y a -- a -> y
-> Into y b -- b -> y
contramap b2a (Into a2y) =
Into (\b -> a2y (b2a b))
For the divide, we combine the data from a and b using the
monoid of y:
instance Monoid y => Divisible (Into y) where
divide :: (c -> (a, b))
-> Into y a -- a -> y
-> Into y b -- b -> y
-> Into y c -- c -> y
divide c2ab (Into a2y) (Into b2y) =
Into (\c -> let (a, b) = c2ab c
in (a2y a) <> (b2y b))
For conquer, the "benign instance" is the mempty value of the monoid,
which by definition does not "interact" with any element, as
mempty <> m = m and m <> mempty = m:
conquer :: Into y a -- a -> y
conquer = Into (\a -> mempty)
In all of these examples, we have (a) A data structure that can be decomposed: this is
the part of c -> (a, b), and (b) A consumer of data: f a is "something that can consume an a.
The laws for Contravariant
So far, I have been skating on intuition, without telling you what the laws Divisible must follow
are. Let's get formal now. For a given Contravariant f, we need a fmap-like law to hold:
fmap's law:: `fmap (f . g) = fmap f . fmap gcontramap's law:contramap (f . g) = contramap g . contramap f
See that the order gets flipped in comparison to fmap. Let us check that
this law holds for Into y, since that was the most general example.
contramap :: (p -> q) -> Into y q -> Into y p
x2q :: x -> q
contramap (x2q . p2x) $ (Into q2y) =?=
contramap p2x . conramap x2q $ (Into q2y)
We can rewrite our Into y definition to be easier to manipulate using
point-free style:
instance Contravariant Into where
contramap :: (b -> a)
-> Into a -- a -> y
-> Into b -- b -> y
contramap b2a (Into a2y) = Into (a2y . b2a) -- b -> y
if we now try to simplify:
contramap p2x . contramap x2q $ (Into q2y)- Remove
.and$:contramap p2x (contramap x2q (Into q2y)) - unwrap inner
contramap: `contramap p2x (Into (q2y . x2q)) - unwrap outer
contramap:Into (q2y . x2q . p2x) - re-group
.:contramap:Into (q2y . (x2q . p2x)) - introduce back
contramap:contramap (x2q . p2x) (Into q2y)
thus we are done! We've shown that the Contravariant laws hold for Into
The laws for Divisible
The laws follow from some category theory. We need that for the function:
delta :: a -> (a, a)
delta a = (a, a)
the following relations between divide and conquer hold:
- First, let us think about
divide delta. It means that we perform the same action on the left element and right element of the tuple since our tuple is built from the same elementa.
dd :: Divisible f => f a -> f a -> f a
dd = divide delta
```
1. `conquer` is an identity element for `divide delta`:
```hs
dd m conquer = dd conquer m
```
2. `divide delta` is associative:
```hs
dd m (dd n o) = dd (dd m n) o
```
So this is saying that `divide delta` is monoidal, with `conquer`
as the identity element. Let's verify what happens in our case of `Into y`.
0. Let `a2y, a2y' :: Into y a`.
1. Expand the definition: `dd (a2y, a2y') = divide delta (a2y, a2y')`
2. Expand `divide`:
```hs
divide delta a2y, a2y'
= Into (\c -> let (a, b) = delta c
in (a2y a) <> (a2y' b))
```
3. Substitue `delta c = (c, c)`
```hs
divide delta a2y, a2y'
= Into (\c -> let (a, b) = (c, c)
in (a2y a) <> (a2y' b))
```
4. Replace `a, b` with `c`
```
divide delta a2y, a2y' = Into (\c -> (a2y c) <> (a2y' c))
```
Great, so we have a simple enough definition of what `dd` does; It runs
both `a2y` and `a2y'` ou the same input and smashes the results. At this
point, it should be hopefully _somewhat_ clear why the laws hold for `Into`:
1. We build `conquer` using `mempty`, Since `mempty` is the identity for `(<>)`,
`conquer should be the identity for `divide delta`.
2. We are smashing outputs using `(<>)` in `divide delta`. As `(<>)` is associative, we should get
associativity of `divide delta` for free.

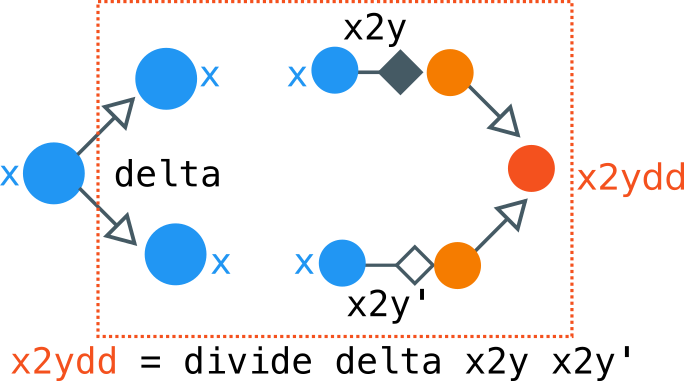
Pictorially, we are combining two machines: one that turns `x2y`, and one that is `conquer` which is "useless". Since we start by copying `x` using `delta x = (x, x)`, whatever `conquer` does is useless, and then only effect that's leftover is whatever the `x2y` does. So we can simplify the above figure by eliminating the bottom part of the computation, leaving us with this:

**Enjoyed this article? [Sign up](https://functional.works-hub.com/register?utm_source=blog&utm_medium=cta&utm_campaign=blog-sign-ups) to Functional Works for more resources like this!**
WorksHub
Jobs
Locations
Articles
Ground Floor, Verse Building, 18 Brunswick Place, London, N1 6DZ
108 E 16th Street, New York, NY 10003
Subscribe to our newsletter
Join over 111,000 others and get access to exclusive content, job opportunities and more!