Thought Experiment: Patching up B-Trees for performance

Thought Experiment: Patching up B-Trees for performance

Recently I came upon a limitation with Database Indexes using B-tree(to be specific B+tree).

Here is the first scenario —

Consider, Customer Orders sample data with the following schema in a MongoDB database and we have an index on the created_at* field.*

{
   "id"         : <String>
   "created_at" : <Timestamp>
   "updated_at" : <Timestamp>
   "status"     : <Integer>
   "items"      : <Array of item-ids>
}

Now, I want to fetch all the orders created on a certain day. I don’t want to burden the database, hence I will paginate this data with page-size and page-number.

There are other approaches for pagination as well but let’s stick to this approach for the sake of API backward compatibility.

I’ll use the following query to get results from the MongoDB:

db.orders.find({"created_at" : {"$gte": timestamp1
                                "$lt" : timestamp2}})
         .skip(page-size*page)
         .limit(page-size)

The above command says —

• Get all the records that have been created between timestamp1 and timestamp2.

• Skip first *page-sizepage records.

• Limit the results to page-size.

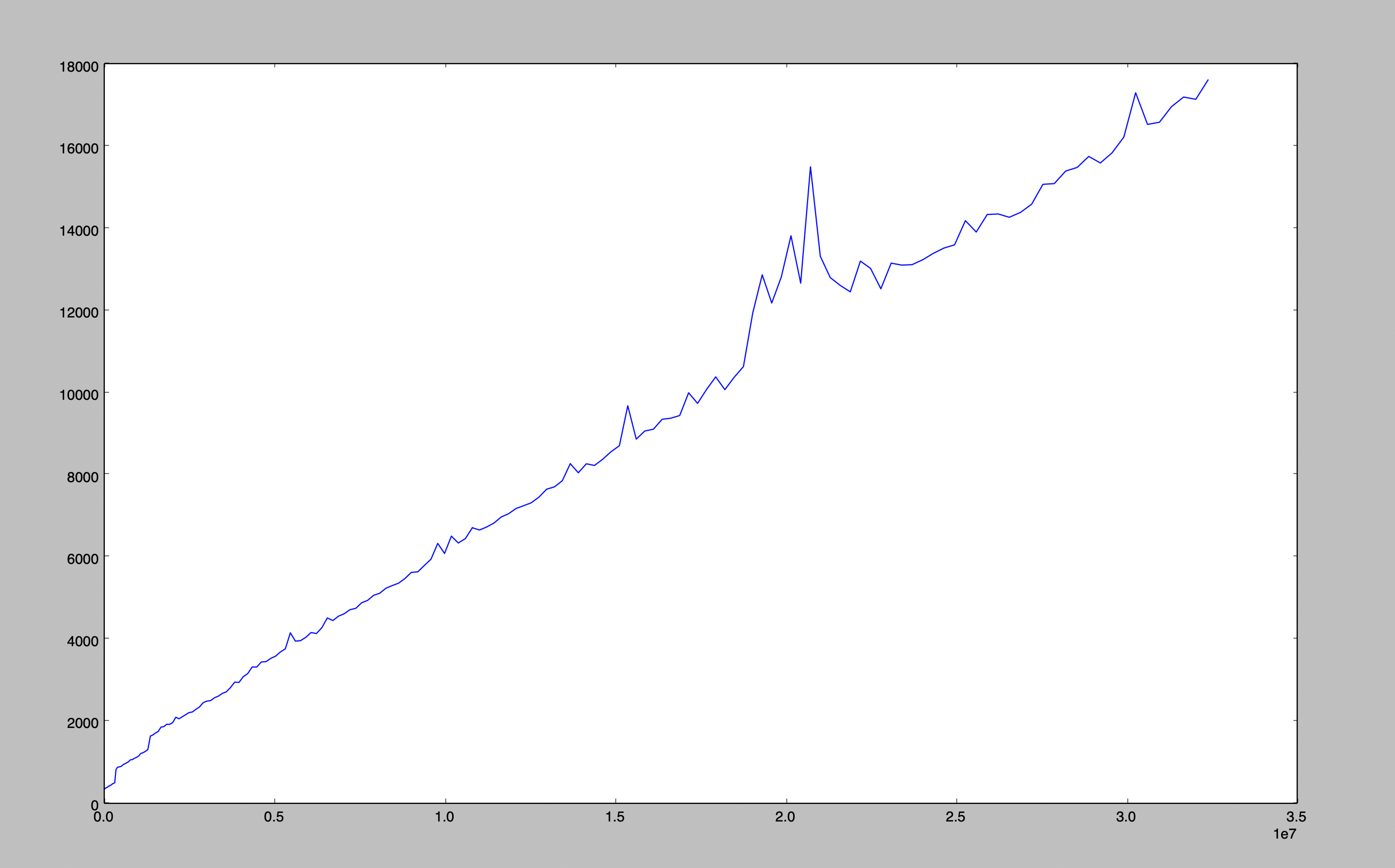
Now, as the skip value starts increasing, the latency starts increasing. It may happen that at the start this query took less than one second and can go up to minutes by the end.

We are hitting the index every time so why is the latency increasing?

To understand why is this happening let’s dive deep into the Data Structure used here to create the index i.e B+ Tree.

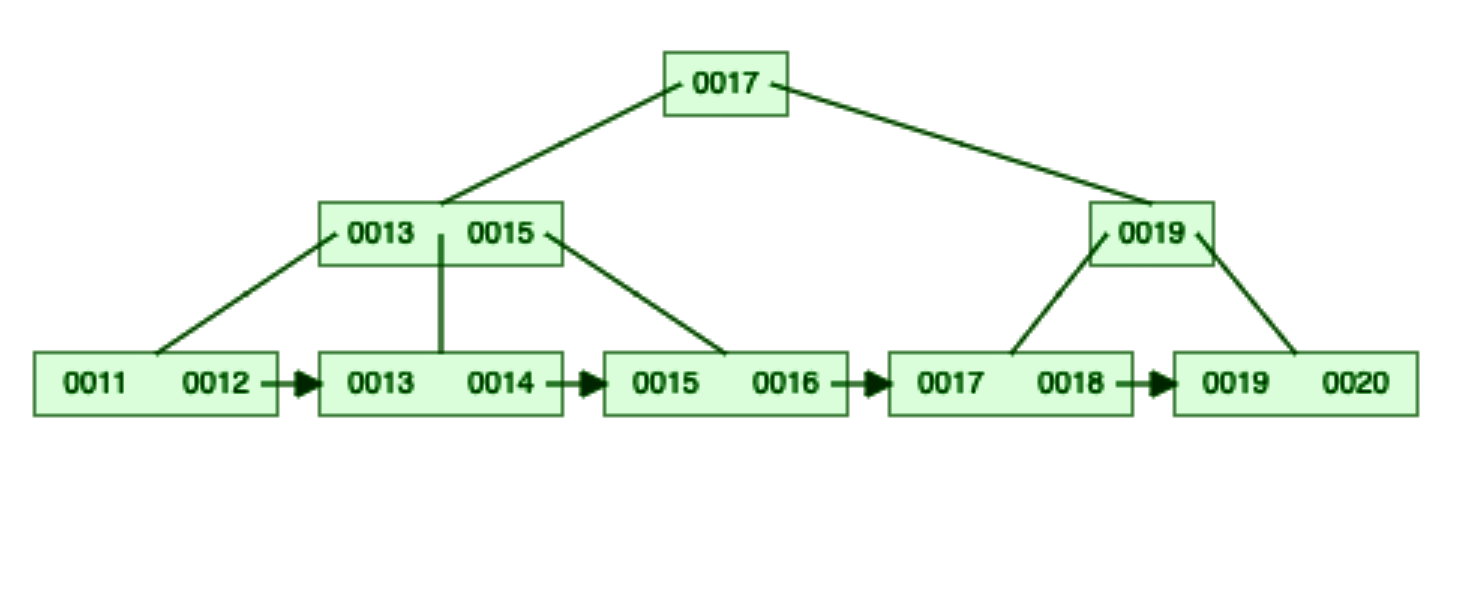
B+ tree is an m-ary tree with a variable but often large number of children per node. Databases store hundreds of keys in a single node. It lets database to find a key with minimum traversal. Best thing about B+ Tree is that it can reside in Main Memory and Disk as well. So, if the Index is getting large and can’t fully reside on Main Memory then lower level nodes will be created in disk. source: Wikipedia

In the above tree, let’s perform our query. Keep page-size as 2 and page as 0. We will keep increasing the page by 1 for each iteration.

+-----------+------+-------+
| Iteration | Skip | Limit |
+-----------+------+-------+
|         1 |    0 |     2 |
|         2 |    2 |     2 |
|         3 |    4 |     2 |
|         4 |    6 |     2 |
|         5 |    8 |     2 |
+-----------+------+-------+

In the last iteration database fetches 10 records from the index then drops the first 8 records and returns the remaining 2 records.

In this case, the database has no way of avoiding tree traversal. The database had no use for the first 8 records but still, it ended up fetching them. Now, Imagine these records are stored in the disk then it will be really costly read operation, and for what?

Another similar scenario — Consider the following Database query:

db.orders.find( { "created_at" : {"$gte": timestamp1
                                  "$lt" : timestamp2}})
         .count()

The above command says —

• Count all the records that have been created between timestamp1 and timestamp2.

To count all the records between the given time range, the database has to read each and every leaf node matching the condition. In a large dataset, it is highly probable that leaf nodes are residing in the disk. So again it is going to be a costly operation.

Modified B+ Tree

We have seen two scenarios where the database is unnecessarily reading from the disk.

In the B+ Tree, the internal node has the following structure —

+-----+----+-----+----+-----+----+-----+
| ref | 11 | ref | 12 | ref | 13 | ref |
+-----+----+-----+----+-----+----+-----+

The keys are surrounded by references to other nodes. Left reference of key points to a node that has smaller values and right reference points to a node that has equal or larger values.

To avoid unnecessary reads, I propose the following improvement to the above structure.

+-----------+----+-----------+----+-----------+----+-----------+
| ref,count | 11 | ref,count | 12 | ref,count | 13 | ref,count |
+-----------+----+-----------+----+-----------+----+-----------+

You can see that I have added count alongside the reference. This count represents the number of keys stored in the reference’s sub-tree.

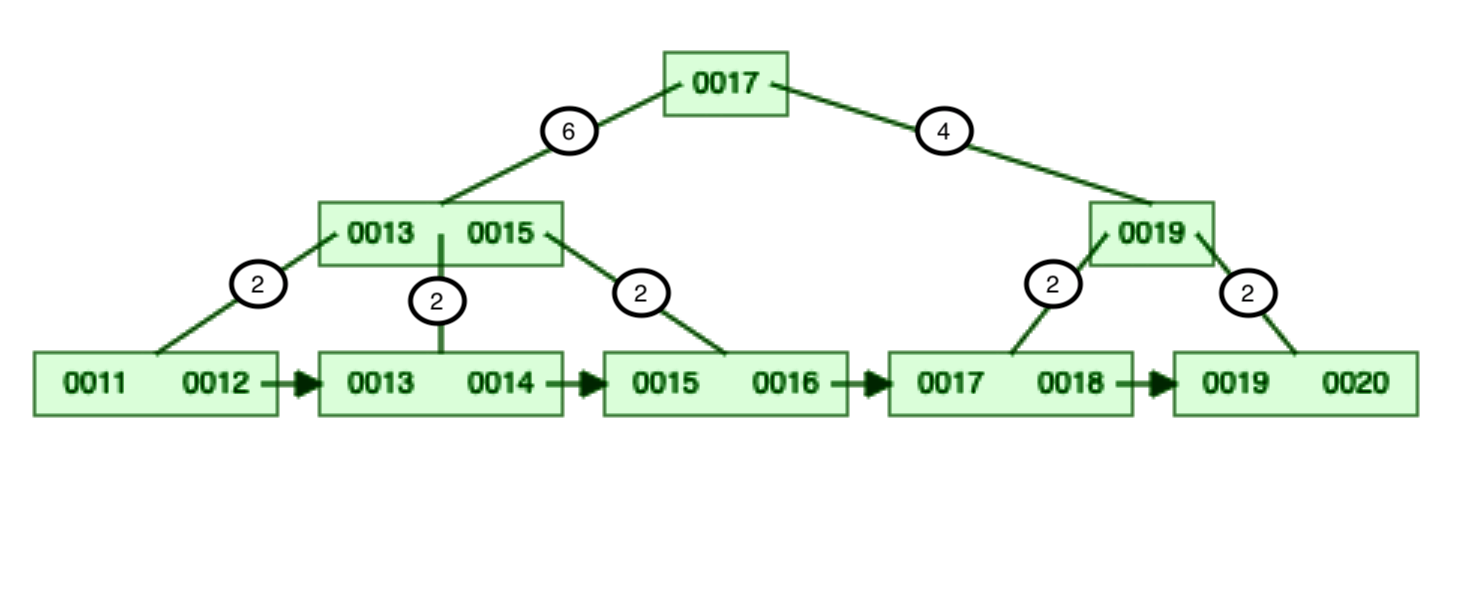
You can see the count attached to each internal node reference in Image 2.

Now let’s re-run the two discussed scenarios on this modified structure.

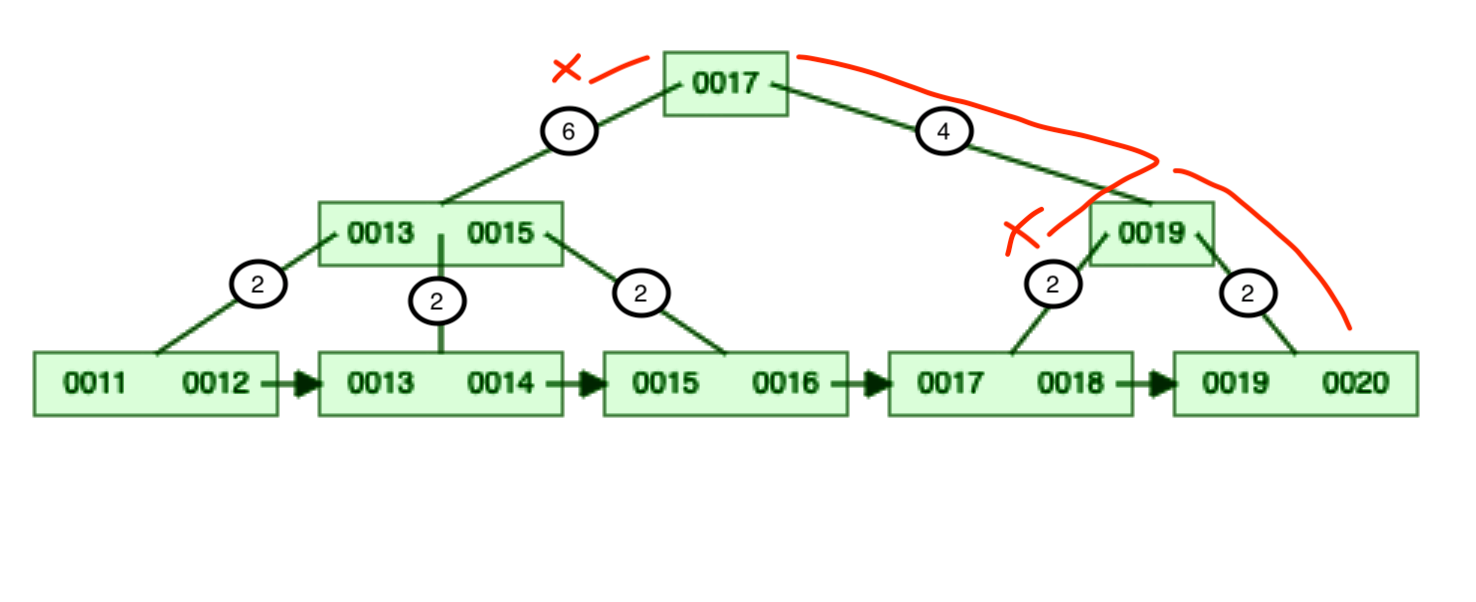
In the first scenario, we want to skip certain records. Taking the same example If I want to skip the first 8 records in the modified structure then —

• Start from the root node i.e. 0017.

• Look at the left reference’s count, it has 6 total keys so we can skip traversing the left subtree altogether. 🎊

• We go to the right subtree node i.e. 0019.

• Again look at the left reference’s count, it has 2 keys so we can skip traversing the left subtree. 🎊

• Now, we have skipped a total of 8 keys so we can pick the remaining 2 keys from the right subtree.

Comparison: We have done only 2 reads with modified B+ Tree in comparison to 7 reads in the original B+ Tree. This is a huge performance improvement for reads.

In the second scenario, we want to count records matching certain conditions. If I want to count records less than 0017, then I just need to traverse to the root node’s left subtree and sum all the reference counts.

Comparison: We have done 1 read with a modified B+ Tree in comparison to 4 reads in the original B+ Tree. This is again amazing performance gain.

Maintenance Cost ⛽️

We have seen amazing read performance gain for the discussed scenarios but there is a cost for maintaining such structure. We have to update the reference count every time a node’s size is updated. This will mean all of the parent nodes until root will be updated as well. Databases generally use a high Degree B+ Tree, hence the depth is nominal. So this shouldn’t be much of a problem.

Closing Remarks

This is a promising structure with great performance improvement for read-heavy workloads. I didn’t get time to implement and benchmark it. Please share your thoughts on it.

Cheers!